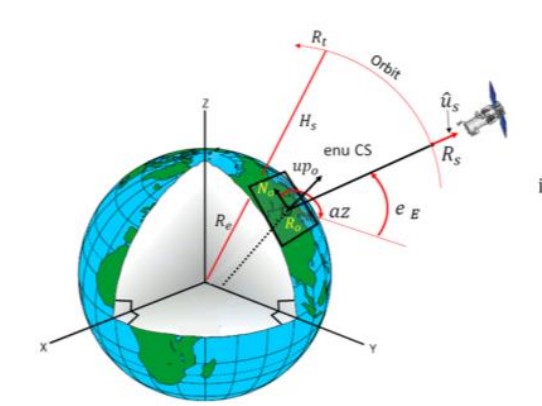
This article describes an investigation of the source of geospatial error in digital surface models (DSMs) constructed from multiple satellite images. In this study, the uncertainty in surface geometry is separated into two spatial components: global error that affects the absolute position of the surface and local error that varies from surface point to surface point. The global error component is caused by inaccuracy in the satellite imaging process, mainly due to uncertainty in the satellite position and orientation (pose) during image collection. The key sources of local error are lack of surface appearance texture, shadows, and occlusion. These conditions prevent successful matches between the corresponding points in the images of a stereo pair. A key result of the investigation is a new algorithm for determining the absolute geoposition of the DSM that reflects the pose covariance of each satellite during image collection. This covariance information is used to weigh the evidence from each image in the computation of the global position of the DSM. The use of covariance information significantly decreases the overall uncertainty in global position and results in a 3-D covariance matrix for the global accuracy of the DSM. This covariance matrix defines a confidence ellipsoid within which the actual error must reside. Moreover, the absolute geoposition of each image is refined to the reduced uncertainty derived from the weighted evidence from the entire image set. This article also describes an approach to the prediction of local error in the DSM surface. The observed variance in surface position within a single stereo surface reconstruction defines the local horizontal error. The variance in the fused set of elevations from multiple stereo pairs at a single DSM location defines the local vertical error. These accuracy predictions are compared to ground truth provided by light detection and ranging (LiDAR) scans of the same geographic region of interest. The prediction of global and local error is compared to the actual errors for several geographic locations and mixes of satellite type. The predicted error bounds contain the observed errors according to the allowed percentage of outliers.